Lesson 0 - High School Stuff (Part 7: Trigonometric Identities)
A trigonometric identity is a relation betweem two different mathematical functions that involve trigonometric functions such as sin(x). They come in handy when simplifying mathematical expressions.
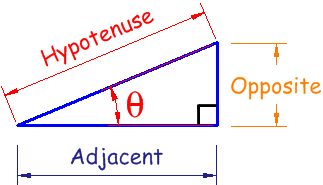
So you know how sin(x)=opposite/hypotenuse of an angle on a right-angle triangle, right? And cos(x)=adjacent/hypotenuse, and tan(x)=opposite/adjacent?
Well there's three others:
Hey, let's look back to Pythagorus's Theorem. O^2+A^2=H^2. We can get three trigonometric identities from this:
Honestly, only the first of those really gets used.
Another useful set of identities is the dual-angle identities. When you have a trigonometric function where the input involves two angles, you can convert it into a different expression, and vice versa.



These identities are helpful when, for example, you know the value of one angle but not the other.
A trigonometric identity is a relation betweem two different mathematical functions that involve trigonometric functions such as sin(x). They come in handy when simplifying mathematical expressions.
So you know how sin(x)=opposite/hypotenuse of an angle on a right-angle triangle, right? And cos(x)=adjacent/hypotenuse, and tan(x)=opposite/adjacent?

Well there's three others:
- csc(x)=H/O=1/sin(x). This is the cosecant.
- sec(x)=H/A=1/cos(x). This is the secant.
- cot(x)=A/O. This is the cotangent.
Hey, let's look back to Pythagorus's Theorem. O^2+A^2=H^2. We can get three trigonometric identities from this:
- Divide by H^2 on both sides. That gets you [sin(x)]^2+
[cos(x)]^2=1. - Divide by A^2 on both sides. That gets you [tan(x)]^2+1=[sec(x)]^2.
- Divide by O^2 on both sides. That gets you 1+[cot(x)]^2=[csc(x)]^2.
Honestly, only the first of those really gets used.
Another useful set of identities is the dual-angle identities. When you have a trigonometric function where the input involves two angles, you can convert it into a different expression, and vice versa.



These identities are helpful when, for example, you know the value of one angle but not the other.
Last edited by Cephalo the Pod on Mon 22 Aug 2016, 2:44 pm; edited 5 times in total



» "It's the door..... To the light" - The Social Thread v 2.0
» Diary of a Mac Student
» Arcasia: Legend of the Wolfram Emerald
» Le Cinéma
» Ideas
» Musique Lystoux
» Through Shady Lanes
» King of All Ratings Thread
» Where's The Beats!?